The NAF range ruler is wrong, and I can prove it.
We all know and love the NAF range ruler. Fair. Clear. Unambiguous. We love it so much in fact, that if there was a problem with two of its squares, we would be obliged to act. To step in. To point them out and fix them.
What’s the distance from (0, 0) to (0, 13)?
We’re going to talk in squares. How many squares is it from (0,0) to (0,13)? The obvious answer is 13. And in this case the obvious answer is happily the correct one. In case you want a little more proving:
Distance from (0,0) to (0,1) is 1, distance from (0,0) to (0,2) is 2 and so on. So the distance from (0,0) to (0,13) is 13. Easy. 13 is a Long Bomb.
So what’s the distance from (0,0) to (5,12) ?
This one is a little trickier. We know that the distance is 5 across and 12 up. We can work out the direct distance by Pythagoras:

So the distance from (0,0) to (5, 12) is also exactly 13. Just like (0,13).
But (5, 12) is at a different angle! – doesn’t matter. Any line through the centre divides a square exactly in half.
13 was a Long Bomb for (0, 13), but it’s out of range for (5, 12)! what’s going on?
How do we fix this?
Option C - 13.04
 |
Similar shape to NAF grid.
4 more Long Bomb squares.
|
Any of these three would be an improvement. Fair, clear, unambiguous and geometrically sound.
Try your own thresholds
The spreadsheet for this article is available here
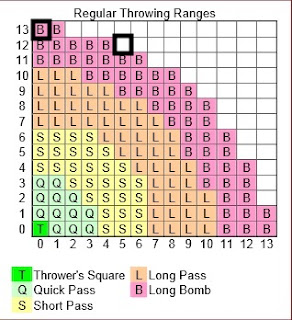








You don't need the proof. The range ruler shows (5,12), (12,5), (7,11) and (11,7) completely in range. :) New player, so I don't know why this is so. Was the ruler changed?
ReplyDelete