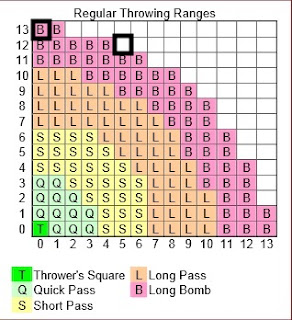
The NAF range ruler is fine and I was wrong

The NAF range ruler is fine and I was wrong

The Internet is a great place for making bold claims based on faulty assumptions, so that's exactly what I did.  In my previous rant I claimed that the NAF range ruler was wrong, proving that two particular squares are the same distance from the thrower's square, but one is in range and one is out.

What did I assume wrong?

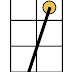
It turns out that the distance between the centre of the thrower's square to the centre of the catcher's square is not the right distance to look at.  The CRP  says:

"Next, the coach must measure the range using the range ruler, by placing the O at on end over the centre of the square of the player throwing the ball, and the red line that runs up the centre of the ruler over the centre of the square the ball is being thrown to. If the line between two passing ranges crosses any part of the receiving player’s square, the higher range should be used"

So we have to measure from the Thrower's centre, to the furthest part of the catcher's square (not the centre of it), but along the line through the centre.

Left to right: My centre-to-centre measurement, the real rulebook measurement, my new approximation.

The NAF range ruler is wrong, and I can prove it.

We all know and love the NAF range ruler. Fair. Clear. Unambiguous. We love it so much in fact, that if there was a problem with two of its squares, we would be obliged to act.  To step in. To point them out and fix them.

 It’s these two. (0, 13) -top left - and (5, 12) - the other one.  But what’s the matter with them?  I will now prove in excruciating detail that they are exactly the same distance from the thrower’s square, (0,0).  Consequently, they should either both be Long Bombs, or both out of range.

What’s the distance from (0, 0) to (0, 13)?

We’re going to talk in squares.  How many squares is it from (0,0) to (0,13)? The obvious answer is 13.  And in this case the obvious answer is happily the correct one.  In case you want a little more proving:

Distance from (0,0) to (0,1) is 1, distance from (0,0) to (0,2) is 2 and so on.  So the distance from (0,0) to (0,13) is 13.  Easy. 13 is a Long Bomb.